Tile: Stückzahl und Selbstkosten | Lineare und Quadratische Funktionen in Anwendungen

Stückzahl und Selbstkosten

Select activity Haben es Schlau und Listig jetzt endlich geschafft...

Haben es Schlau und Listig jetzt endlich geschafft?

„Sie haben doch überhaupt keine Ahnung vom Geschäft. Entlassen sollte man Sie. Umsatz hin, Umsatz her, was interessiert mich der Umsatz? Wir haben doch auch Kosten bei der Herstellung der Aufkleber. Und die müssen sie doch in ihren Berechnungen berücksichtigen. Mit was für Mitarbeitern muss ich mich hier herumschlagen. Informieren Sie sich gefälligst über unsere Kostenstruktur! Wie hoch sind die Selbstkosten bei einer wöchentlichen Stückzahl von 9500 Aufklebern? Und wie viele Aufkleber produzieren wir, wenn unsere Selbstkosten 40000,-€ betragen?“

Schlau und Listig verziehen sich wieder und kramen in den Akten. Die wöchentlichen Selbstkosten, so finden sie heraus, setzen sich zusammen aus den Fixkosten, das ist ein fester Grundbetrag von 24000,-€ für Personal, Maschinenpark, Gebühren, usw., und aus den sogenannten Herstellungskosten, die sich als Produkt aus den sogenannten Stückkosten in Höhe von -,80€ pro Stück für Material, Energie, usw. und der Stückzahl ergeben. Also kann Zickler wohl geholfen werden. Schlau und Listig machen sich wiederwillig an die Arbeit.

Du hast aber bis jetzt gut mitgearbeitet, so dass dir die Lösung dieser Aufgabe leicht fällt.

Bemerkung: Du kannst alle Rechnungen ohne Maßeinheiten durchführen und auch den Funktionsterm bzw. die Funktionsgleichung ohne Maßeinheiten angeben. Du musst aber die Endergebnisse immer mit Maßeinheiten angeben und die Parameter des Funktionsterms mit Maßeinheiten interpretieren können.
Select activity Aufgabe 5.a Markiere – am besten mit einem Textmar...
Aufgabe 5.a

Markiere – am besten mit einem Textmarker – diejenigen Textstellen, die dir für eine mathematische Lösung des Problems wichtig erscheinen.

Lösung

„Sie haben doch überhaupt keine Ahnung vom Geschäft. Entlassen sollte man sie. Umsatz hin, Umsatz her, was interessiert mich der Umsatz? Wir haben doch auch Kosten bei der Herstellung der Aufkleber. Und die müssen sie doch in ihren Berechnungen berücksichtigen. Mit was für Mitarbeitern muss ich mich hier herumschlagen. Informieren sie sich gefälligst über unsere Kostenstruktur! Wie hoch sind die Selbstkosten bei einer wöchentlichen Stückzahl von 9500 Aufklebern? Und wie viele Aufkleber produzieren wir, wenn unsere Selbstkosten 40000,-€ betragen?“

Schlau und Listig verziehen sich wieder und kramen in den Akten. Die wöchentlichen Selbstkosten, so finden sie heraus, setzen sich zusammen aus den Fixkosten, das ist ein fester Grundbetrag von 24000,-€ für Personal, Maschinenpark, Gebühren, usw., und aus den sogenannten Herstellungskosten, die sich als Produkt aus den sogenannten Stückkosten in Höhe von -,80€ pro Stück für Material, Energie, usw. und der Stückzahl ergeben.

Kompetenzen

Mathematisieren eines Sachverhalts.

Aufgabe 5.b

Vervollständige die folgende Tabelle.

Stückzahl z in Stk	13000	14000	15000	16000	17000	19000	21000	23000
Fixkosten f in €	24000	24000	24000	24000	24000	24000	24000	24000
Stückkosten s in €	-,80	-,80	-,80	-,80	-,80	-,80	-,80	-,80
Herstellungskosten h in €
Selbstkosten k in €

Tipp

Die Herstellungskosten sind das Produkt aus Stückzahl und Stückkosten. Die Selbstkosten sind die Summe aus den Fixkosten und den Herstellungskosten.

Lösung

Stückzahl z in Stk	13000	14000	15000	16000	17000	19000	21000	23000
Fixkosten f in €	24000	24000	24000	24000	24000	24000	24000	24000
Stückkosten s in €	-,80	-,80	-,80	-,80	-,80	-,80	-,80	-,80
Herstellungskosten h in €	10400	11200	12000	12800	13600	15200	16800	18400
Selbstkosten k in €	34400	35200	36000	36800	37600	39200	40800	42400

Kompetenzen

Mathematisieren eines Sachverhalts.

Select activity Aufgabe 5.c Erstelle ein dem Problem angemessenes ...
Aufgabe 5.c

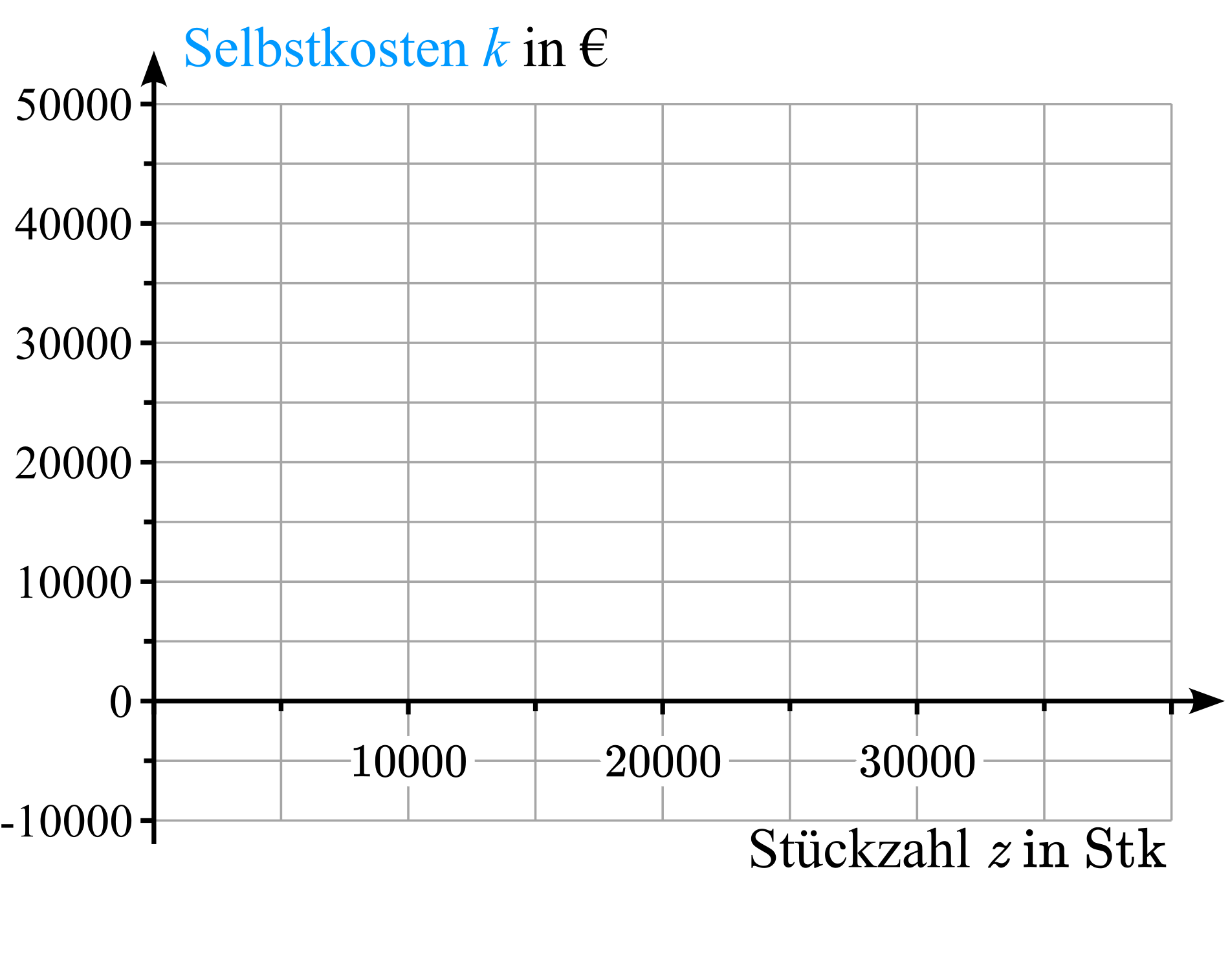
Erstelle ein dem Problem angemessenes Koordinatensystem mit beschrifteten und skalierten Achsen zur Darstellung des Zusammenhangs zwischen der Stückzahl \(z\) und den Selbstkosten \(k\). Dabei soll die Stückzahl auf der Rechtsachse und die Selbstkosten auf der Hochachse aufgetragen werden.

Rechtsachse: 1cm entspricht 2500Stk, Hochachse: 1cm entspricht 2500,-€.

Lösung

Kompetenzen

Anfertigen eines beschrifteten und skalierten Koordinatensystems, das dem Sachzusammenhang angemessen ist.
Select activity Aufgabe 5.d Trage die Wertepaare aus der Tabelle a...
Aufgabe 5.d

Trage die Wertepaare aus der Tabelle als Punkte in das Koordinatensystem ein.

Verbinde die Punkte durch einen Graphen.

Nenne den Typ dieses Graphen.

Lösung

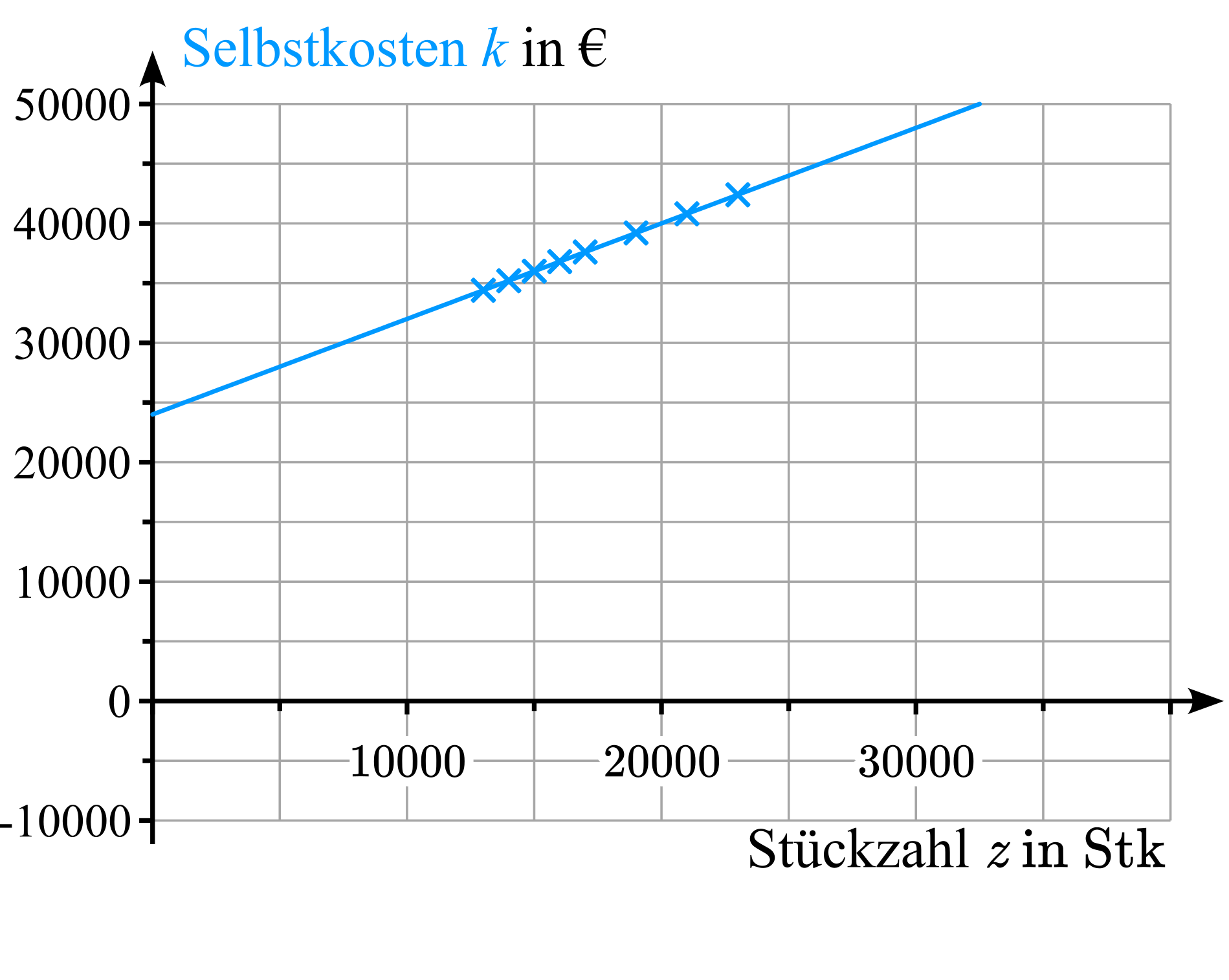
Der Graph ist eine Gerade.

Kompetenzen

Eintragen von Punkten in ein Koordinatensystem

Erkennen eines geradlinigen Verlaufs von Punkten
Select activity Aufgabe 5.e Nenne aufgrund des Graphen den Funktio...
Aufgabe 5.e

Nenne aufgrund des Graphen den Funktionstyp, der den Zusammenhang zwischen der Stückzahl und den Selbstkosten beschreibt.

Gib die allgemeine Form des Funktionsterms und der Funktionsgleichung dieses Funktionstyps an.

Erläutere die Bedeutung der im Funktionsterm vorkommenden Parameter.

Lösung

Der Graph ist eine Gerade. Der Zusammenhang zwischen der Stückzahl \(z\) und den Selbstkosten \(k\) wird durch eine lineare Funktion beschrieben.

Der Funktionsterm lautet \(k\left(z\right) = m \cdot z + n\) und die Funktionsgleichung \(k = m \cdot z + n\).

Dabei ist

\(m\) die Steigung/der Steigungsfaktor und

\(n\) der \(y\)-Achsenabschnitt, d.h. der Wert, an dem der Graph die Hochachse schneidet. Es handelt sich dabei also um den Funktionswert an der Stelle Null.

Kompetenzen

Erkennen einer Geraden als Graph einer Linearen Funktion

Nennen des Funktionsterms einer Linearen Funktion und korrektes Bezeichnen dieses Funktionsterms

Nennen der Funktionsgleichung einer Linearen Funktion

Nennen der Bedeutung der Parameter \(m\) und \(n\) im Funktionsterm einer Linearen Funktion
Select activity Aufgabe 5.f Bestimme auf zwei verschiedenen Wegen ...
Aufgabe 5.f

Bestimme auf zwei verschiedenen Wegen den Funktionsterm , der den Zusammenhang zwischen der Stückzahl \(z\) und dem Kosten \(k\) beschreibt.

1. Weg

Berechne mit zwei bekannten Formeln zuerst den Steigungsfaktor \(m\) und dann den Achsenabschnitt \(n\).

Lösung

Wir nutzen die beiden Punkte \({\rm{P}}(13000|34400)\) und \({\rm{Q}}(17000|37600)\).

\[\begin{array}{l} m = \frac{{37600 - 34400}}{{17000 - 13000}} = \frac{4}{5} = 0,8\\n = 34400 - 0,8 \cdot 13000 = 24000\end{array}\]

Daher lautet der Funktionsterm \(k\left(z\right) = 0{,}8 \cdot z + 24000\).

Kompetenzen

Berechnen der Parameter \(m\) und \(n\) einer Linearen Funktion mit Hilfe von Formeln

2. Weg

Berechne die Parameter \(m\) und \(n\) gleichzeitig mit Hilfe eines Linearen Gleichungssystems.

Lösung

Wir nutzen die beiden Punkte \({\rm{P}}(13000|34400)\) und \({\rm{Q}}(17000|37600)\).

\(\begin{array}{l}{\left| {\begin{aligned} 34400 &= k(13000) \\ 37600 &= k(17000) \end{aligned}} \right.} \end{array}\)

\(\begin{array}{l}{\left| {\begin{aligned}34400 &= m \cdot 13000 + n\\37600 &= m \cdot 17000 + n\end{aligned}} \right.}&{\begin{array}{l}{\left| { \cdot \left( { - 1} \right)} \right.}\\{\left| { + {\rm{I'}}} \right.}\end{array}}\end{array}\)

\(\begin{array}{l}{\left| {\begin{aligned}34400 &= m \cdot 13000 + n\\3200 &= m \cdot 4000\end{aligned}} \right.}&{\begin{array}{l}{}\\{ \Rightarrow m = \frac{3200}{4000} = 0{,}8}\end{array}}&{\left. {\begin{array}{l}{}\\{}\end{array}} \right\} \Rightarrow n = 34400 - 0{,}8 \cdot 13000 = 24000}\end{array}\)

\(\begin{array}{l}{\left| {\begin{aligned} 24000 &= n \\ 0{,}8 &= m \end{aligned}} \right.} \end{array}\)

Lösung mit GeoGebra
k(z):=m*z+n
Löse({34400=k(13000),37600=k(17000)},{m,n})

Daher lautet der Funktionsterm \(k\left(z\right) = 0{,}8 \cdot z + 24000\).

Kompetenzen

Aufstellen eines Linearen Gleichungssystems zur Bestimmung der Parameter \(m\) und \(n\) einer Linearen Funktion mit Hilfe von zwei Punkten

Lösen eines Linearen Gleichungssystems mit zwei Gleichungen und zwei Variablen
Select activity Aufgabe 5.g Überprüfe rechnerisch, ob dein Funktio...
Aufgabe 5.g

Überprüfe rechnerisch, ob dein Funktionsterm den Zusammenhang zwischen der Stückzahl \(z\) und den Selbstkosten \(k\) korrekt beschreibt.

Lösung

Einsetzen der Wertepaare in die Funktionsgleichung \(k = 0{,}8 \cdot z + 24000\) ergibt:

\[\begin{array}{l}34400 = 0,8 \cdot 13000 + 24000 \quad (w)\\36000 = 0,8 \cdot 15000 + 24000 \quad (w)\\37600 = 0,8 \cdot 17000 + 24000 \quad (w)\end{array}\]

Kompetenzen

Überprüfen, ob Wertepaare die Funktionsgleichung einer Linearen Funktion erfüllen.
Select activity Aufgabe 5.h Gib die Werte des Steigungsfaktors \(m...
Aufgabe 5.h

Gib die Werte des Steigungsfaktors \(m\) und des Achsenabschnitts \(n\) mit den jeweiligen Maßeinheiten an.

Erläutere die Bedeutung des Steigungsfaktors \(m\) und des Achsenabschnitts \(n\) im Sachzusammenhang.

Lösung

Der Steigungsfaktor ist \(m = 0{,}8\) bzw. mit Einheiten \(m = 0{,}80\,\frac{\rm{€}}{\rm{Stk}}\).
Wenn man die Stückzahl um 1Stk erhöht, erhöhen sich die Stückkosten um \(0{,}80\,\rm{€}\).

Der Achsenabschnitt ist \(n=24000\) bzw. mit Einheiten \(n=24000,-\rm{€}\).
Wenn man keinen Aufkleber herstellt, betragen die Stückkosten \(24000,-\rm{€}\). Es handelt sich hierbei um die Fixkosten, die unabhängig von der Anzahl der hergestellten Aufkleber sind.

Kompetenzen

Interpretieren des Steigungsfaktors einer Linearen Funktion im Sachzusammenhang

Interpretieren des Achsenabschnitts einer Linearen Funktion im Sachzusammenhang
Select activity Aufgabe 5.i Erstelle mit Hilfe eines Funktionsgrap...
Aufgabe 5.i

Erstelle mit Hilfe eines Funktionsgraphenplotters in einem dem Problem angemessenen Koordinatensystem mit beschrifteten und skalierten Achsen den Funktionsgraphen, der den Zusammenhang zwischen der Stückzahl \(z\) und den Selbstkosten \(k\) graphisch darstellt.

Lösung

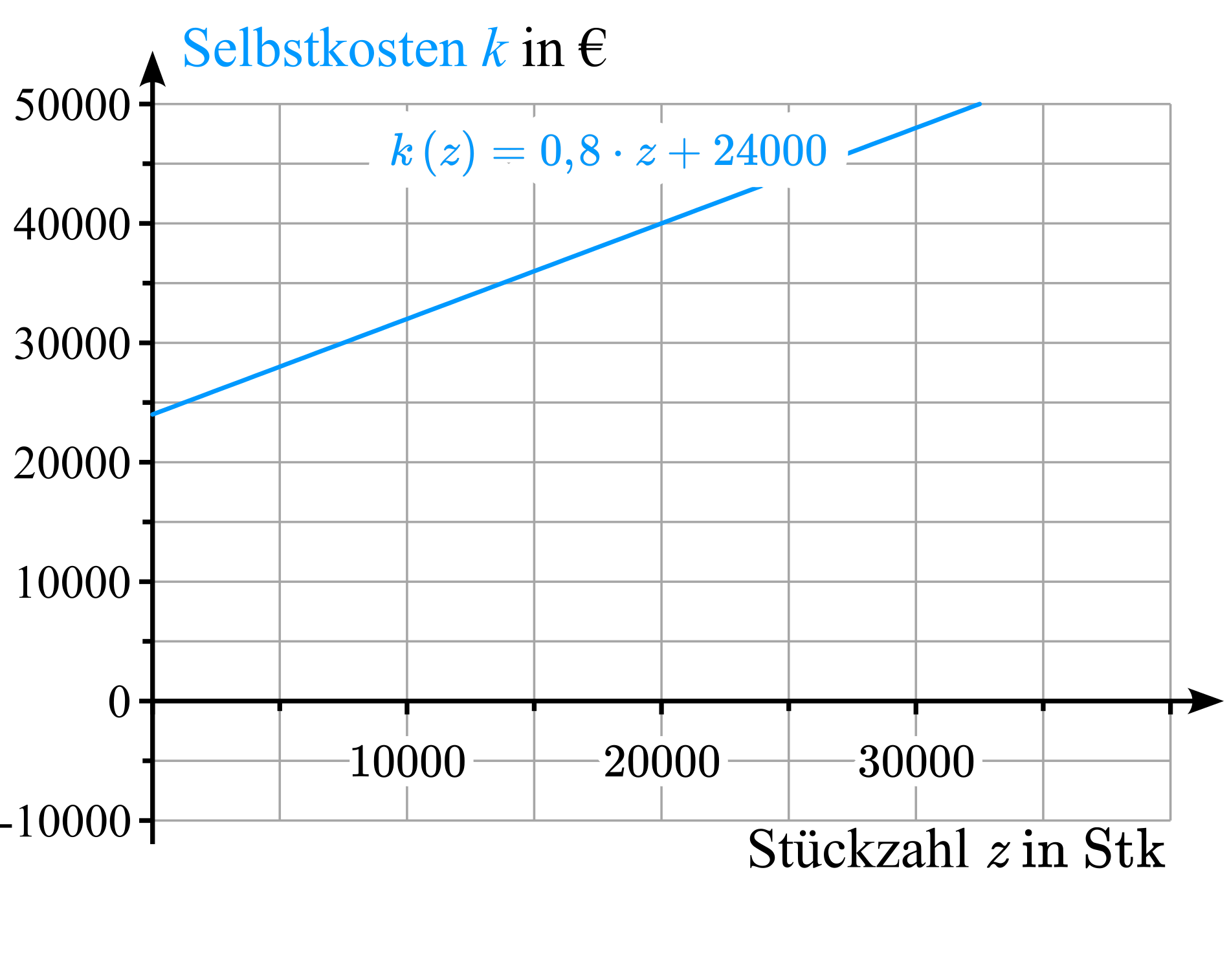
Kompetenzen

Erstellen eines Funktionsgraphen mit Hilfe eines Funktionsgraphenplotters in einem dem Problem angemessenen Koordinatensystem mit beschrifteten und skalierten Achsen
Select activity Aufgabe 5.j Beantworte rechnerisch die erste von H...
Aufgabe 5.j

Beantworte rechnerisch die erste von Herrn Zickler gestellte Frage.

Überprüfe dein Ergebnis anhand der Graphen aus den Aufgaben 5.d bzw. 5.i.

Lösung

Zur Beantwortung der ersten Frage berechnet man den Funktionswert zur Stelle 9500, setzt also 9500 in den Funktionsterm ein und berechnet den Termwert.

\[k\left( {9500} \right) = 0{,}8 \cdot 9500 + 24000 = 7600 + 24000 = 31600\]

Lösung mit GeoGebra
k(z):=0.8*z+24000 k(9500)

Bei einer wöchentlichen Produktion von 9500 Aufklebern belaufen sich die Selbstkosten auf 31600,-€.

Das Ergebnis lässt sich am Graphen bestätigen.

Kompetenzen

Mathematisieren eines Sachverhalts

Berechnen eines Funktionswertes zu einer vorgegebenen Stelle einer Linearen Funktion

Berechnen des Wertes eines Linearen Terms
Select activity Aufgabe 5.k Beantworte rechnerisch die zweite von ...
Aufgabe 5.k

Beantworte rechnerisch die zweite von Herrn Zickler gestellte Frage.

Überprüfe dein Ergebnis anhand der Graphen aus den Aufgaben 5.d bzw. 5.i.

Lösung

Zur Beantwortung der zweiten Frage berechnet man die Stelle zum Funktionswert 40000, setzt also den Funktionsterm gleich 40000 und bestimmt die Lösungsmenge der entstehenden Gleichung.

\[\begin{aligned}k\left( z \right) &= 40000\\0{,}8 \cdot z + 24000 &= 40000 \quad \left| { - 24000} \right.\\0{,}8 \cdot z &= 16000 \quad \left| {:0{,}8} \right.\\z &= 20000\\L &= \left\{ {20000} \right\}\end{aligned}\]

Lösung mit GeoGebra
k(z):=0.8*z+24000 Löse(k(z)=40000,z)

Die Selbstkosten betragen 40000,-€, wenn 20000 Aufkleber produziert werden.

Das Ergebnis lässt sich am Graphen bestätigen.

Kompetenzen

Mathematisieren eines Sachverhalts

Berechnen der Stelle zu einem vorgegebenen Funktionswert einer Linearen Funktion

Bestimmen der Lösungsmenge einer Linearen Gleichung

Stückzahl und Selbstkosten

Aufgabe 5.a

Aufgabe 5.b

Aufgabe 5.c

Aufgabe 5.d

Aufgabe 5.e

Aufgabe 5.f

1. Weg

2. Weg

Aufgabe 5.g

Aufgabe 5.h

Aufgabe 5.i

Aufgabe 5.j

Aufgabe 5.k