Lineare und Quadratische Funktionen in Anwendungen
-
Stückzahl und Stückpreis - Teil 2
-
Nachdem Schlau und Listig ihre Ergebnisse vorgetragen haben, ist Zickler aber nicht zufrieden:
„Das kann doch nicht wahr sein, zeigen Sie doch wenigstens einmal ein klein wenig Eigeninitiative! Bildchen malen können Schüler der Klasse 5 auch. Was haben Sie denn in der Schule in der Klasse 8 gemacht? Ich will den Funktionsterm, der den Zusammenhang zwischen der Stückzahl und dem entsprechenden Stückpreis beschreibt. Und ich erwarte natürlich auch, dass Sie mir meine beiden Fragen, nämlich was wir für einen Aufkleber verlangen könnten, wenn wir wöchentlich nur noch 9500 Stück herstellen wollen, und wie viel Aufkleber wir wöchentlich produzieren könnten, wenn wir den Preis auf 1,85€ senken, rechnerisch beantworten. Wehe, wenn Ihnen das nicht gelingt.“
Bevor ihnen weiteres Ungemach droht, machen sich Schlau und Listig davon und beginnen direkt mit der Arbeit. Du warst in der Klasse 8 natürlich aufmerksam, so dass dir die notwendigen Berechnungen leicht fallen.
Bemerkung: Du kannst alle Rechnungen ohne Maßeinheiten durchführen und auch den Funktionsterm bzw. die Funktionsgleichung ohne Maßeinheiten angeben. Du musst aber die Endergebnisse immer mit Maßeinheiten angeben und die Parameter des Funktionsterms mit Maßeinheiten interpretieren können.
-
Aufgabe 2.a
Nenne aufgrund des in Aufgabe 1.e gezeichneten Graphen den Funktionstyp, der den Zusammenhang zwischen der Stückzahl und dem Stückpreis beschreibt.
Lösung
Der Graph ist eine Gerade. Der Zusammenhang zwischen Stückzahl und Stückpreis wird also durch eine Lineare Funktion beschrieben.
Kompetenzen
- Erkennen einer Geraden als Graph einer Linearen Funktion
-
Aufgabe 2.b
Gib die allgemeine Form des Funktionsterms und der Funktionsgleichung dieses Funktionstyps an.
Erläutere die Bedeutung der im Funktionsterm vorkommenden Parameter.
Lösung
Der Funktionsterm einer Linearen Funktion lautet allgemein \(m \cdot x + n\) und wird meist mit \(f(x)\) bezeichnet. Man schreibt dann \(f(x)=m \cdot x +n\).
Dabei ist
-
\(m\) die Steigung/der Steigungsfaktor und
-
\(n\) der Achsenabschnitt (oft auch \(y\)-Achsenabschnitt), d.h. der Funktionswert zur Stelle 0, an dem der Graph die Hochachse schneidet. Hinweis: Die Stellen, an denen der Graph die Rechtsachse schneidet, bezeichnet man als Nullstellen.
Allgemein lautet die Funktionsgleichung jeder Funktion \(y=f(x)\). Die Funktionsgleichung einer Linearen Funktion lautet dann wegen \(f(x)=m \cdot x +n\) gemein \(y=m \cdot x +n\).
In unserem konkreten Beispiel mit den Variablen \(z\) und \(p\) lautet der Funktionsterm \(m \cdot z + n\), wir bezeichnen ihn mit \(p(z)\) und schreiben \(p(z) = m \cdot z + n\).
Die Funktionsgleichung lautet dann \(p = m \cdot z + n\).
Kompetenzen
- Nennen des Funktionsterms einer Linearen Funktion und korrektes Bezeichnen dieses Funktionsterms
- Nennen der Funktionsgleichung einer Linearen Funktion
- Nennen der Bedeutung der Parameter \(m\) und \(n\) im Funktionsterm einer Linearen Funktion
-
-
Aufgabe 2.c
Bestimme auf zwei verschiedenen Wegen den Funktionsterm , der den Zusammenhang zwischen der Stückzahl \(z\) und dem Stückpreis \(p\) beschreibt.
1. Weg
Berechne mit zwei bekannten Formeln zuerst den Steigungsfaktor \(m\) und dann den Achsenabschnitt \(n\).
Tipp
Sind \({\rm{P}}(x_1|y_1)\) und \({\rm{Q}}(x_2|y_2)\) zwei Punkte einer Geraden, dann berechnet man den Steigungsfaktor \(m\) durch
\(m=\frac{y_2-y_1}{x_2-x_1}\)
und den Achsenabschnitt \(n\) durch
\(n=y_1-m \cdot x_1\)
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Wir nutzen die beiden Punkte \({\rm{P}}(13000|2{,}7)\) und \({\rm{Q}}(17000|2{,}3)\), setzen die Koordinaten der beiden Punkte in die Formeln ein und erhalten
\(\begin{array}{l} m = \frac{{2,3 - 2,7}}{{17000 - 13000}} = - \frac{1}{{10000}} = - 0,0001\\n = 2,7 - \left( { - 0,0001} \right) \cdot 13000 = 4\end{array}\)
Daher lautet der Funktionsterm \(p(z) = - 0{,}0001 \cdot z + 4\).
Kompetenzen
- Berechnen der Parameter \(m\) und \(n\) einer Linearen Funktion mit Hilfe von Formeln
2. Weg
Berechne die Parameter \(m\) und \(n\) gleichzeitig mit Hilfe eines Linearen Gleichungssystems.
Tipp
Sind \({\rm{P}}(x_1|y_1)\) und \({\rm{Q}}(x_2|y_2)\) zwei Punkte einer Geraden, dann muss für diese beiden Punkte die Funktionsgleichung wahr sein, d.h. die beiden folgenden Gleichungen müssen erfüllt sein.
\(\left| \begin{array}{l}{y_1} = m \cdot {x_1} + n\\{y_2} = m \cdot {x_2} + n\end{array} \right.\)
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Wir nutzen die beiden Punkte \({\rm{P}}(13000|2{,}7)\) und \({\rm{Q}}(17000|2{,}3)\) und setzen die Koordinaten der Punkte in die Funktionsgleichung ein.
\(\begin{array}{l}{\left| {\begin{aligned} 2{,}7 &= p(13000) \\ 2{,}3 &= p(17000) \end{aligned}} \right.} \end{array}\)
\(\begin{array}{l}{\left| {\begin{aligned} 2{,}7 &= m \cdot 13000 + n\\ 2{,}3 &= m \cdot 17000 + n\end{aligned}} \right.}&{\begin{array}{l}{\left| { \cdot \left( { - 1} \right)} \right. \rightarrow {\rm{I'}}:\; -2{,}7 = -m \cdot 13000 - n \quad }\\{\left| { + {\rm{I'}}} \right.}\end{array}}\end{array}\)
\(\begin{array}{l}{\left| {\begin{aligned} 2{,}7 &= m \cdot 13000 + n\\ -0{,}4 &= m \cdot 4000\end{aligned}} \right.}&{\begin{array}{l}{}\\{ \Rightarrow m = \frac{-0{,}4}{4000} = -0,0001}\end{array}}&{\left. {\begin{array}{l}{}\\{}\end{array}} \right\} \Rightarrow n = 2{,}7 + 0{,}0001 \cdot 13000 = 4}\end{array}\)
\(\begin{array}{l}{\left| {\begin{aligned} 4 &= n \\ -0{,}0001 &= m \end{aligned}} \right.} \end{array}\)
Lösung mit GeoGebra
p(z):=m*z+nLöse({2.7=p(13000),2.3=p(17000)},{m,n})Daher lautet der Funktionsterm \(p(z) = - 0{,}0001 \cdot z + 4\).
Kompetenzen
- Aufstellen eines Linearen Gleichungssystems zur Bestimmung der Parameter \(m\) und \(n\) einer Linearen Funktion mit Hilfe von zwei Punkten
- Lösen eines Linearen Gleichungssystems mit zwei Gleichungen und zwei Variablen
-
Aufgabe 2.d
Überprüfe rechnerisch, ob dein Funktionsterm den Zusammenhang zwischen der Stückzahl und dem Stückpreis korrekt beschreibt.
Tipp
Setze einige Wertepaare aus der Tabelle aus Aufgabe 1.b in die Funktionsgleichung ein.
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Einsetzen dreier Wertepaare in die Funktionsgleichung \(p = - 0{,}00001 \cdot z + 4\) ergibt
\(\begin{array}{l}2{,}7 = - 0{,}0001 \cdot 13000 + 4\quad(w)\\2{,}5 = - 0{,}0001 \cdot 15000 + 4\quad(w)\\2{,}3 = - 0{,}0001 \cdot 17000 + 4\quad(w)\end{array}\)Kompetenzen
- Überprüfen, ob Wertepaare die Funktionsgleichung einer Linearen Funktion erfüllen.
-
Aufgabe 2.e
Gib die Werte des Steigungsfaktors \(m\) und des Achsenabschnitts \(n\) mit den jeweiligen Maßeinheiten an.
Erläutere die Bedeutung des Steigungsfaktors und des Achsenabschnitts im Sachzusammenhang.
Lösung
Der Steigungsfaktor ist \(m = \frac{-1}{10000} = -0{,}0001\) bzw. mit Einheiten \(m = \frac{-1}{10000}\,\frac{\rm{€}}{\rm{Stk}}\).
Wenn die Firma wöchentlich 10000 Aufkleber mehr verkaufen möchte, muss sie den Stückpreis um 1,-€ senken bzw. wenn die Firma den Stückpreis um 1,-€ senkt, kann sie wöchentlich 10000 Aufkleber mehr verkaufen.Der Achsenabschnitt ist \(n=4\) bzw. mit Einheiten \(n=4,-\rm{€}\).
Wenn die Firma keine Aufkleber mehr herstellt, könnte sie (rein theoretisch) einem Stückpreis von 4,-€ verlangen.Kompetenzen
- Interpretieren des Steigungsfaktors einer Linearen Funktion im Sachzusammenhang
- Interpretieren des Achsenabschnitts einer Linearen Funktion im Sachzusammenhang
-
Aufgabe 2.f
Erstelle mit Hilfe eines Funktionsgraphenplotters in einem dem Problem angemessenen Koordinatensystem mit beschrifteten und skalierten Achsen den Funktionsgraphen, der den Zusammenhang zwischen der Stückzahl \(z\) und dem Stückpreis \(p\) graphisch darstellt.
Lösung
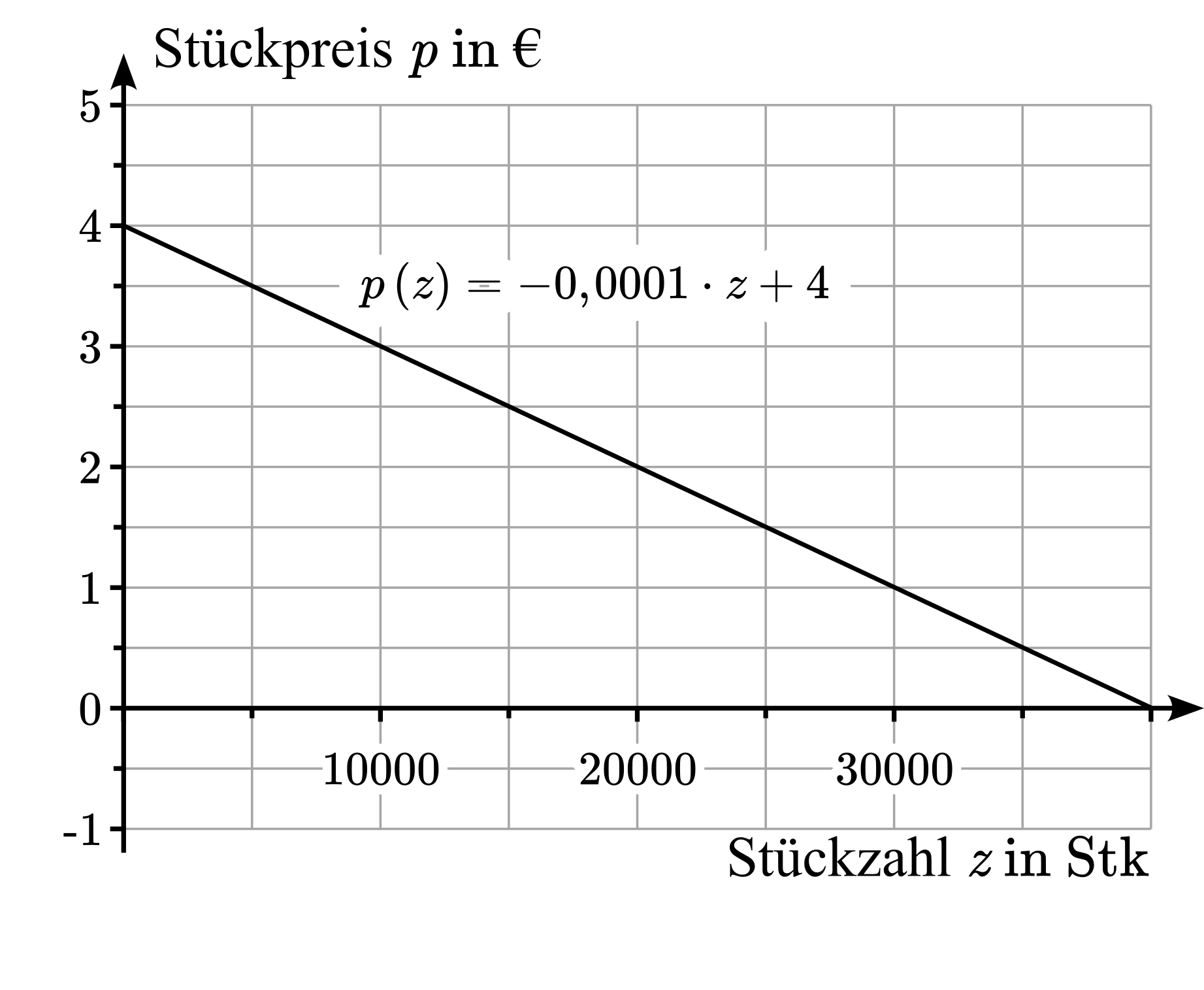
Kompetenzen
- Erstellen eines Funktionsgraphen mit Hilfe eines Funktionsgraphenplotters in einem dem Problem angemessenen Koordinatensystem mit beschrifteten und skalierten Achsen
-
Aufgabe 2.g
Berechne, welchen Stückpreis die Firma (rein theoretisch) verlangen könnte, wenn sie überhaupt keine Aufkleber mehr herstellen würde.
Vergleiche das Ergebnis mit dem aus Aufgabe 1.f.
Tipp
Berechne den Achsenabschnitt.
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Man berechnet den Funktionswert zur Stelle 0, setzt also 0 in den Funktionsterm ein und berechnet den Termwert.
\(p(0) = -0{,}0001 \cdot 0 + 4 = 4\)Lösung mit GeoGebra
p(z):=-0.0001*z+4p(0)Wenn man keine Aufkleber mehr herstellen würde, könnte man (rein theoretisch) einen Stückpreis von 4,-€ verlangen.
Das Ergebnis stimmt mit dem aus Aufgabe 1.f überein.
Kompetenzen
- Mathematisieren eines Sachverhalts
- Berechnen eines Funktionswertes zu einer vorgegebenen Stelle einer Linearen Funktion
- Berechnen des Wertes eines Linearen Terms
-
Aufgabe 2.h
Berechne, welche Stückzahl die Firma (rein theoretisch) an Aufklebern loswürde, wenn sie diese verschenken würde.
Vergleiche das Ergebnis mit dem aus Aufgabe 1.g.
Tipp
Berechne die Nullstelle.
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Zur Beantwortung der Frage berechnet man die Stelle zum Funktionswert 0, setzt also den Funktionsterm gleich 0 und bestimmt die Lösungsmenge der entstehenden Gleichung.
\(\begin{aligned}p(z) &= 0\\- 0,0001 \cdot z + 4 &= 0 && | - 4\\ - 0,0001 \cdot z &= - 4 && |:\left( { - 0,0001} \right)\\ z &= 40000\\L &= \left\{ {40000} \right\}\end{aligned}\)Lösung mit GeoGebra
p(z):=-0.0001*z+4
Löse(p(z)=0,z)Wenn man die Aufkleber verschenken (also den Preis auf 0,-€ senken) würde, könnte man 40000Stk verschenken.
Das Ergebnis stimmt mit dem aus Aufgabe 1.g überein.
Kompetenzen
- Mathematisieren eines Sachverhalts
- Berechnen der Stelle zu einem vorgegebenen Funktionswert einer Linearen Funktion
- Bestimmen der Lösungsmenge einer Linearen Gleichung
-
Aufgabe 2.i
Beantworte rechnerisch die erste von Herrn Zickler gestellte Frage.
Vergleiche das Ergebnis mit dem aus Aufgabe 1.h.
Tipp
Du musst den Funktionswert zu einer Stelle berechnen.
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Zur Beantwortung der Frage berechnet man den Funktionswert zur Stelle 9500, setzt also 9500 in den Funktionsterm ein und berechnet den Termwert.
\(p(9500) = -0{,}0001 \cdot 9500 + 4 = 3{,}05\)Lösung mit GeoGebra
p(z):=-0.0001*z+4
p(9500)Wenn die Firma wöchentlich 9500 Aufkleber herstellt, kann sie für einen Aufkleber 3,05€ verlangen.
Das Ergebnis stimmt mit dem aus Aufgabe 1.h überein.
Kompetenzen
- Mathematisieren eines Sachverhalts
- Berechnen eines Funktionswertes zu einer vorgegebenen Stelle einer Linearen Funktion
- Berechnen des Wertes eines Linearen Terms
-
Aufgabe 2.j
Beantworte rechnerisch die zweite von Herrn Zickler gestellte Frage.
Vergleiche das Ergebnis mit dem aus Aufgabe 1.i.
Tipp
Du musst die Stelle zu einem Funktionswert berechnen.
Erklärvideo
Datenschutzhinweis
Sobald das hier eingebettete Video abgespielt wird, erhält YouTube als externer Anbieter diese Daten von Ihnen übermittelt.Lösung
Zur Beantwortung der zweiten Frage berechnet man die Stelle zum Funktionswert 1,85, setzt also den Funktionsterm gleich 1,85 und bestimmt die Lösungsmenge der entstehenden Gleichung.
\(\begin{aligned}p(z) &= 1,85\\- 0,0001 \cdot z + 4 &= 1{,}85 && | - 4\\ - 0,0001 \cdot z &= - 2,15 && |:\left( { - 0,0001} \right)\\ z &= 21500\\L &= \left\{ {21500} \right\}\end{aligned}\)Lösung mit GeoGebra
p(z):=-0.0001*z+4Löse(p(z)=1.85,z)Wenn die Firma den Preis auf 1,85€ senkt, kann sie wöchentlich 21500 Aufkleber verkaufen.
Das Ergebnis stimmt mit dem aus Aufgabe 1.i überein.
Kompetenzen
- Mathematisieren eines Sachverhalts
- Berechnen der Stelle zu einem vorgegebenen Funktionswert einer Linearen Funktion
- Bestimmen der Lösungsmenge einer Linearen Gleichung
-